CP Violation in the B-system

Quark mixing in the standard model is described by the Cabibbo-Kobayashi-Maskawa (CKM) matrix [1], eqn(1). Conventionally the $u,c {\rm\ and\ } t$ quarks are unmixed and the mixing is described by the $3\times 3\; V_{CKM}$ matrix operating on the $d,s {\rm\ and\ } b$ quarks. The matrix elements of V_CKM can, in principle, be determined by measuring the charged current coupling to the $W^{\pm}$ bosons.  

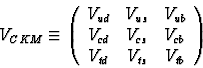
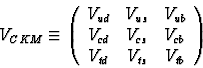$$V_{CKM} \equiv \left( \begin{array} {ccc} V_{ud} & V_{us} & ... ... V_{cs} & V_{cb} \ V_{td} & V_{ts} & V_{tb} \end{array}\right)$$ (1)

The CKM matrix is unitary ie $V_{CKM}^{\dagger}V_{CKM} = 1,$ which leads to 9 unitarity conditions expressed in terms of the matrix elements. There are several (approximate) parameterisations of the CKM matrix, one of the more popular approaches is that of Wolfenstein [2], eqn(2), where the matrix elements are expressed in terms of powers of $\lambda = \sin \theta_c,$ where $\theta_c$ is the Cabibbo angle. As can be seen from this parameterisation, the 9 complex elements of the matrix can be expressed in terms of 4 independent variables; three real parameters $A, \lambda {\rm \ and\ }\rho$ and an imaginary part of a complex number, $\eta.$ The 18 parameters of the CKM matrix can be reduced to 4 because of the unitarity constraints and the arbitrary nature of the relative quark phases [3]. It is the complex phase in the V_CKM that leads to CP violation in the standard model.

 

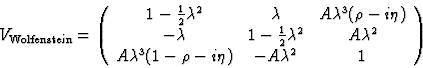$$V_{\rm Wolfenstein} = \left( \begin{array} {ccc} 1-\frac{1}{... ... A\lambda^3(1-\rho - i\eta) & -A\lambda^2 & 1\end{array}\right)$$ (2)

The unitarity condition

V_udV_ub^* + V_cdV_cb^* + V_tdV_tb^* = 0

is of particular interest since $V_{ud} \simeq V_{tb} \simeq 1$ and $V_{ts}^* \simeq -V_{cb}.$ This allows us to depict this condition as a triangle in the complex plane, as shown in fig 1. The angles of the triangle $\alpha, \beta {\rm \ and\ } \gamma$ are related to the phase and can be measured in CP violating B-decays.

  

Figure 1: The CKM unitarity triangle in the Wolfenstein parameterisation

The non-closure of this triangle ie $\alpha + \beta + \gamma \ne \pi$ would suggest that our understanding of CP violation within the Standard Model was incomplete. Physics beyond the Standard Model can be further investigated, for example, by measuring CP asymmetries in several B decays that depend on the same unitarity angle or studying decays where zero asymmetries are expected in the Standard Model.

CP violation in the B system should be observable through the phenomenon of $B^0 - \bar{B^0}$ mixing, see for example [4]. This $B^0 - \bar{B^0}$ mixing is dominated by box-diagrams with virtual $t-{\rm quarks},$fig 2.

  

Figure 2: $B^0 - \bar{B^0}$ mixing diagrams.

The following decays

are into a CP eigenstate. If this is coupled with only a single diagram contributing to the decay, CP asymmetries can be constructed which are directly related to the angles of the unitarity triangle. For example, these conditions occur for the decay mode $B^0_d \rightarrow J/\psi K^0_s.$Here the number of B⁰_d which decay at time t (where t is expressed in units of lifetime) is proportional to  

$$n(t) \propto e^{-t}(1 + \sin 2\beta \sin xt)$$ (3)

and the number of $\bar{B^0_d}$ is proportional to  

$$\bar{n}(t) \propto e^{-t}(1 - \sin 2\beta \sin xt)$$ (4)

where the mixing parameter, $x=\Delta M/\Gamma\simeq 0.67,$ is the ratio of the mass difference of the eigenstates to their decay rate. The CP asymmetry can then be defined as

$$a(t) = \frac{n(t) - \bar{n}(t)}{n(t) + \bar{n}(t)} = \sin 2\beta \sin xt.$$

By integrating eqns. (4) and (5) over time a similar asymmetry can be constructed which is proportional to $\sin 2\beta$. (Although for coherent B production ie the $B \bar{B}$ pair is produced in a definite CP state, this time integrated asymmetry is zero.) In addition this channel is experimentally very promising because of the dilepton decay of the $J/\psi.$Unfortunately additional decay diagrams contribute to the other channels listed in eqn(3) so there is no longer a complete cancellation of the hadronic matrix elements in the CP asymmetry. The $B^0_d \rightarrow \pi^+ \pi^-$ channel, which is dependent on the angle $\alpha$ is predicted to have large hadronic corrections from `penguin' diagrams, fig. 3. The $B^0_s \rightarrow \rho K^0_s$ (dependent on the angle $\gamma$) also has additional hadronic contributions but, in addition, suffers from a very low branching fraction. Fortunately there are, of course, many other channels which can be used to measure CP violation, eg see ref. [5].

  

Figure 3: `Penguin' contribution to $B^0_d \rightarrow \pi^+ \pi^-$ decay